C++ Notes - Hex Converter

Background

When I use OpenGL to develop a game engine and write a renderer for it, I often encounter the need to write an independent shader file and store the glsl code in a text file.

However, the file in text format is slow to read, and the file size is relatively large (even after zip compression), and at the same time, to encapsulate the shader and hide it from the engine user, I need to design a binary file format myself, and write an unique IO system for it.

In this context, the conversion between binary and decimal is particularly important. To understand the conversion between bases, I tried to use the least code to write a converter.

---

Implementation

The main idea is to first convert the input number to a decimal number. And then, convert the decimal number into the desired number.

The implementation looks like this:

void HexConverter(char* in, int s_in, char* out, int s_out)
{
    int v = 0, n;
    // Convert the input into a decimal number
    for(char* p = in; *p; p++)
        v = v * s_in + (*p - (( *p >= 'a' ) ? ('a' - 10) : '0'));
    // Convert the decimal number to s_out based number
    for(n = 31; v && n; v = v / s_out)
        out[n--] = (((v % s_out) < 10) ? '0' : ('a' - 10)) + (v % s_out);
    // Copy the answer to the output array
    memmove(out, out + n + 1, 32 - n - 1);
    // Cut the output array
    out[32 - n - 1] = 0;
}

The converter falls into two parts:

1. First part

// Convert the input into a decimal number
for(char* p = in; *p; p++)
    v = v * s_in + (*p - (( *p >= 'a' ) ? ('a' - 10) : '0'));

• The first for-loop is used to convert the input into a decimal number.
  • *p represents the number on each digit of the input number.
  • Use *p as the condition statement, so that the loop won’t stop until p points to ‘\0’ which equals false and also represents the end of the array.

v = v * s_in + (*p - (( *p >= 'a' ) ? ('a' - 10) : '0'));

• This line is where the math gets in.
  • (( *p >= ‘a’ ) ? (‘a’ - 10) : ‘0’) figures out whether the digit is a character.
    • If it is, this part would return ‘a’ - 10. Then the right part of this code would turn into *p - ‘a’ + 10.
    • If it isn’t, this part would return ‘0’. Then the right part of this code would turn into *p - ‘0’.
    • By doing so, the digit is converted to a decimal number. (0123456789abcdef is the sequence of the digits)
  • This line could be simplified as: v = v * s_in + decimal format of current digit.
    • After the iteration, this line endd up like: v = (…((v * s + d) * s + d) * s + d) * s … + d.
    • s_ins in each layer are cumulative, they would add up and become $\sum_{i=1}^{n} v_is^{n+1-i}$. And this is exactly the representation of an s-based number in decimal.

2. Second Part

• The algorithm follows the steps listed below:
  1. Divide the decimal number by s_out.
  2. Write down the remainder (in the desired base).
  3. Divide the result again by s_out.
  4. Repeat steps 2 and 3 until the result is 0.
  5. The result is the digit sequence of the remainder from the last to the first.

// Convert the decimal number to s_out based number
for(n = 31; v && n; v = v / s_out)
    out[n--] = (((v % s_out) < 10) ? '0' : ('a' - 10)) + (v % s_out);

• The second for-loop is used to convert the decimal number into the desired base.
  • n is the iteration index. Since the upper bound of int is $2^{32}$, the output array cannot be longer than 32. (index range: 0-31)
  • v && n make sure the converter won’t convert numbers bigger than $2^{32}$. n would be out of range if the input is bigger than $2^{32}$.
  • v = v / s_out represents step 1

out[n--] = (((v % s_out) < 10) ? '0' : ('a' - 10)) + (v % s_out);

• n– represents “digit sequence from the last to first”.
• v % s_out is the remainder, < 10 checks whether it would be a character.
  • If it would, returns ‘a’ - 10 and add it with the reminder to convert it.
  • If it won’t, returns ‘0’ and add it with the reminder so the number will not change, only the type would become char.

---

Conclusion

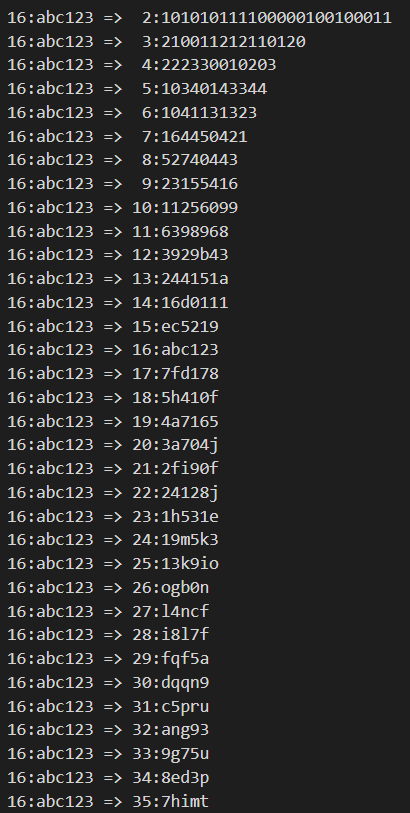
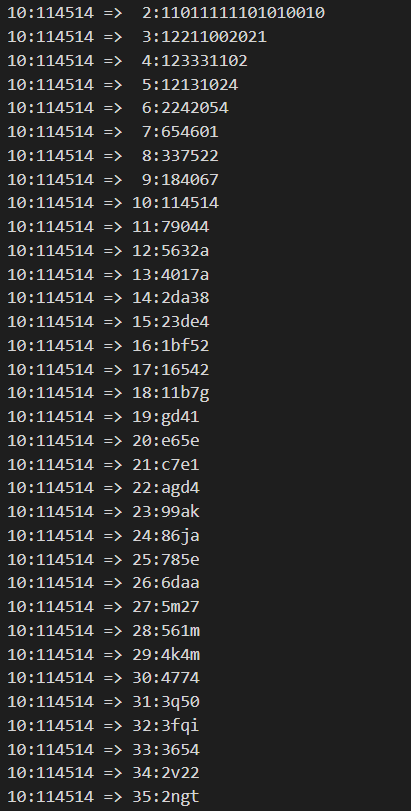
This converter works for all base-conversion between binary, octal decimal, and hexadecimal numbers.

Test Code:

int main()
{
    char out[33];
    for(int s = 2; s < 36; s++)
    {
        HexConverter("abc123", 16, out, s);
        printf("16:abc123 => %2d:%s\n", s, out);
    }
    for(int s = 2; s < 36; s++)
    {
        HexConverter("114514", 10, out, s);
        printf("10:114514 => %2d:%s\n", s, out);
    }
}

Test Result: